Fractal Home
The source code is hyperbolic.js. Thanks to Eric Rowell for the library KineticJS. Watch the HTML source code of this page, too. There is an experimental version with images...
The Hyperbolic Machine
The basic construction consists of the hyperbolic triangle with the angles α, β and γ given by natural numbers k, n, m as fractions of 180°.
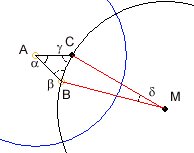
α = 180°/k, β = 180°/n and
γ = 180°/m with the condition
1/k + 1/m + 1/n < 1
The traingle has two straight lines AB and AC and an arc side BC. You controll the situation of the points A (yellow), B (orange) by moving the small circles in the drawing area. The machine then completes the construction. The point C is calculated under the condition of the given angles. α is measured normally and the angles β and γ are measured between the straight lines and the circle line tangents. The sum of the three angle values has to be less than 180°. As a second condition the circle line of BC with center M (white) outside has to cut the circle with centre A vertically.
Therefor the angle δ and the centre M of the construction circle is given. The blue fixed circle cuts the construction circle around M vertically. If the angles of the hyperbolic triangle are given by natural numbers k, m, n, so that the conditions are like noticed left then we have some interesting results:
- All picture triangles produced as iterated reflections at the triangle sides of the basic triangle itself, give a complete tesselation of the blue circle. They don't cover each other and only contact at its borders.
- The resulting triangle corners are from the same order as the corners of the basic hyperbolic triangle.
The machine is easy to use. Chose the natural numbers k, n und m without hurting the condition above. If the image looks too "dotty", let draw again or increase the values for dots and iterations.
