L-Systeme - Pflanzen
Geschichte und Funktionsweise eines L-Systems
1968 begann der deutsche Biologe Aristid Lindenmayer (Bild N° 1) ein Modell zu entwickeln, das mit Hilfe einiger weniger "Produktionsregeln" Pflanzenwachstum beschreibt. Dieses Modell wird heute Lindenmayer-System oder kurz L-System genannt. Im Amerikanischen ist auch der Begriff "Parallel Rewriting System" gebräuchlich. Zwei weitere Pioniere auf dem Gebiet der L-Systeme und Wachstumssimulationen waren der Mathematiker Grzegorz Rozenberg und der Informatiker Premyszlaw Prusinkiewicz.

Bild N° 1: Aristid Lindenmayer (1925 - 1989)
Das Grundprinzip eines L-Systems ist denkbar einfach: Beginnend mit
einem Startelement generieren wir, eben mit Hilfe der Produktionsregeln
Elementketten, die dann graphisch darzustellen sind. Ein solches Element
kann ein Blatt, eine Knospe, ein Stück Stengel, etc. sein. Jedes Element
kann Parameter enthalten, die Größe, Alter, Farbe, Hormonkonzentration
o.ä. beschreiben können. Aufgrund seiner Einfachheit ist das
L-System sehr gut für eine Übertragung auf den Computer geeignet.
Das alles erfordert jedoch eine riesige Menge an mathematischen Definitionen,
die zum Teil recht schwer formulierbar sind.1
1Für ausführliche Definitionen siehe Lindenmayer, A. und Rozenberg, G.: Automata, Languages and Development.
In unseren Beispielen und Modellen werden wir verschiedenartige L-Systeme gebrauchen, die wir der Übersicht halber hier auflisten und stichwortartig beschreiben:
- Deterministische L-Systeme, bzw. nicht deterministische oder stochastische L-Systeme. Stochastische L-Systeme enthalten Zufallselemente, Deterministische nicht. Deterministische L-Systeme kennzeichnet man mit einem "D"
- Kontext freie, bzw. Kontext sensitive L-Systeme. Bei Kontext sensitiven L-Systemen hängt die Entwicklung der einzelnen Elemente von ihren Nachbarn ab, nicht so bei den Kontext freien. Je nach Größe des berücksichtigten Kontextes werden die L-Systeme mit 1, 2, 3... gekennzeichnet. 0 steht für Kontext freie.
- 1D, 2D oder 3D Interpretation der Zeichenketten. Je nach Interpretationsdimension sind unterschiedliche Produktionsregeln nötig.
- Parametrische oder nicht parametrische L-Systeme. Enthalten die einzelnen Elemente Parameter oder Indexe, so ist ein L-System als parametrisch zu bezeichnen.
Wir beginnen mit der einfachsten Form von L-Systemen, den 0L-Systemen (sprich
Null-L-System). 0L-System, das bedeutet, dass sich jedes Element des Systems
unabhängig von seinen Nachbarn entwickelt. Man spricht darum auch
von einem Kontext freien L-System (amerik. Deterministic Context-free
L-System). Kontext sensitive L-Systeme behandeln wir später.
Zu unterscheiden ist im Moment zwischen deterministischen D0L-Systemen
und nicht deterministischen 0L-Systemen.
Definition eines 0L-Systems (nicht deterministisch) und eines D0L-Systems (deterministisch):

Man lasse sich von dieser Definition nicht einschüchtern. Anhand des folgenden bekannten und sehr einfachen Beispiels zeigen wir auf praktischem Weg die Funktionsweise eines eindimensionalen D0L-Systems auf.
Die blaugrüne Bakterie Anabaena Catenula formiert sich zu
einer sogenannten Schwingfadenalge, d.h. eine eindimensionale Kette von
Bakterien. Unter dem Mikroskop sieht sie wie eine Reihe unterschiedlich
langer Zylinder aus.
Für das Wachstum von Anabaena Catenula sind Elemente aus
zwei verschiedenen Bakterientypen verantwortlich, die sich durch ihre Größe
sowie durch ihr Teilungsverhalten unterscheiden. Nennen wir sie A und B.
Da beide Typen asymmetrisch aufgebaut sind, können sie in der
Kette entweder nach links oder nach rechts orientiert sein. Es gibt daher
aus praktischer Sicht vier unterschiedliche Elemente, nämlich:
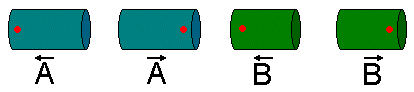
Bild N° 2: Bakterientypen von Anabaena Catenula
Das Alphabet V unseres ersten L-Systems beschränkt sich also auf
vier Zeichen: 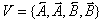 .
(Im Grunde kann jedes graphische Symbol als Zeichen dienen.)
.
(Im Grunde kann jedes graphische Symbol als Zeichen dienen.)
Eine nach rechts orientierte A-Bakterie teilt sich nach einer gewissen
Zeit in eine nach rechts orientierte B-Bakterie und in eine nach links
orientierte A Bakterie. Wir schreiben formal die erste Produktionsregel
p1
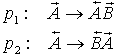 und demzufolge p2 genau spiegelverkehrt:
und demzufolge p2 genau spiegelverkehrt:
B-Bakterien werden nach einer gewissen Zeit zu A-Bakterien
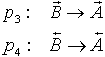 und damit haben wir jedem Symbol a unseres Alphabets V ein nichtleeres Wort
und damit haben wir jedem Symbol a unseres Alphabets V ein nichtleeres Wort 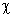 zugeordnet.
zugeordnet.
Wir schreiben  und nennen a den Vorgänger und
und nennen a den Vorgänger und 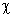 den
Nachfolger.
den
Nachfolger.
Aus jedem Wort, das aus den Symbolen des Alphabets gebildet werden kann,
können wir genau ein neues Wort erzeugen, in dem wir (zur gleichen
Zeit!) alle Symbole des Wortes als Vorgänger annehmen und diese durch
ihre Nachfolger ersetzen.
Aus dem erhaltenen Wort können wir wiederum mit demselben Verfahren
ein neues bilden (Iteration). Eine Serie solcher aufeinander folgender
Wörter nennen wir Sequenz.
Was jetzt noch fehlt, ist eine Startbakterie, von der das Wachstum
ausgeht. Diese Startbakterie nennen wir Axiom. Ihr wird der Formelbuchstabe ω
zugeordnet und sie ist das erste Wort der zu erzeugenden Sequenz.
In manchen Büchern wird anstatt von Axiom und Produktionsregeln
von Initiator und Generator gesprochen, wobei das Axiom der Initiator und
die Menge aller Produktionsregeln der Generator ist.
Die Entwicklung von Anabaena Catenula kann also zusammenfassend
in folgendem L-System beschrieben werden:
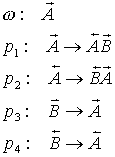
Vom Axiom ausgehend erhalten wir eine Sequenz von Zeichenketten, die verschiedenen
Wachstumsstadien von Anabaena Catenula entsprechen.
Einen besseren Eindruck der Gesamtform erhält man, indem man die
Zeichen interpretiert, das heißt durch diejenigen graphischen Elemente
ersetzt, denen sie zugeordnet worden sind (Siehe Bild N° 3). Im Moment
ist das noch sehr einfach.
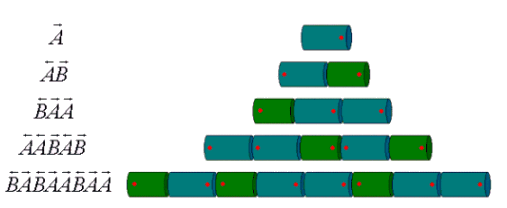
Bild N° 3: Anabaena Catenula Modell 1
Man beachte, dass in diesem Modell die genaue Zeit, in der sich die Bakterien teilen sowie das Wachstum der einzelnen Bakterien noch nicht berücksichtigt wurde.
Im Labor wurde beobachtet2, dass die
größere A-Bakterie sich etwa alle 15 Stunden teilt. Die kleineren
B-Bakterien werden nach etwa drei Stunden zu A-Bakterien.
Als Zeiteinheit für ein verbessertes Modell eignet sich also eine
Dauer von 3h. Eine B-Bakterie formt sich also wie gehabt in einer Zeiteinheit
in eine A-Bakterie um. Die Entwicklung einer A-Bakterie teilen wir in 5 Schritte auf:
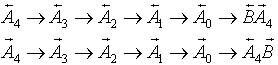
Wir erweitern damit das Alphabet auf: 
Als verbessertes Modell können wir also das folgende L-System benutzen:
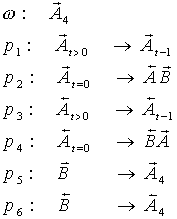
Die graphische Interpretation des verbesserten Modells entspricht ziemlich genau der Wirklichkeit. Man beachte, dass Bakterien verschiedener Stadien sowie verschiedener Generationen koexistieren.
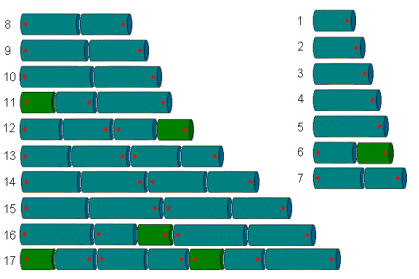
Bild N° 4: Anabaena Catenula Modell 2
2Mitchison G.J. und Wilcox M.: Roule governing cell division in Anabaena Catenula, Nature 239 (1972) S. 110-111 [zurück]
Dies ist die denkbar einfachste Form von L-Systemen, das sogenannte
D0L-System. Es beinhaltet weder Zufallsproduktionsregeln (ist also deterministisch),
noch hängt das Verhalten der einzelnen Elemente von ihren Nachbarn
ab (kontextfrei).
Allerdings kann das zweite Modell bereits als parametrisches L-System
angesehen werden.
Das bisher eindimensionale D0L-System auf zwei (und später drei) Dimensionen auszuweiten, ist eine einfache Sache: Wir brauchen dazu bloß eine Schildkröte. Diese Schildkröte, die unser willenloser Sklave ist, richten wir auf folgende Befehle ab:
F Zeichne Element F und bewege dich um die Länge des Elements
F nach vorne
G Zeichne Element G und bewege dich um die Länge des Elements G nach vorne
... ...
+ Drehe dich um δ gegen den Uhrzeigersinn
- Drehe dich um δ im Uhrzeigersinn
[ Merke deine aktuelle Position
] Kehre zur letztgemerkten Position zurück
Das Alphabet des L-Systems entspricht diesen Befehlen: V = {F, G,
..., +, -, [, ]}
Das Wort F+F+F-F würde also von der Schildkröte als
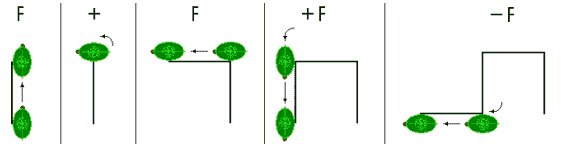
interpretiert (δ = 90°). Das Wort F[+F][-F-F]F als
![Schildkröte interpretiert F[+F][-F-F]F Schildkröte interpretiert F[+F][-F-F]F](lsyspics/einflsys07.gif)
Mit Hilfe der Schildkröteninterpretation (amerik. Turtle interpretation) können wir Verzweigungen jeder Art realisieren. Je mehr Iterationsschritte wir ausführen, desto verästelter wird das Ergebnis sein. Wir präsentieren einige mögliche L-Systeme dieser Art.
Dieses L-System enthält nur ein Element F. F wird von der Schildkröte als grüne Linie interpretiert. Bereits nach der vierten Iteration musste sie 1116 Zeichenbefehle ausführen. Der Parameter δ beträgt 30°. Bei allen folgenden L-Systemen werden wir die Parameter an die Produktionsregeln anhängen.
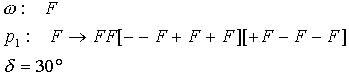

Bild N° 5: Buschige Struktur
Sechs Iterationen, 4607 Zeichen. Allerdings wurden nur alle F gezeichnet;
das Element I ist ausschließlich dazu da, um die Verzweigungen zu
generieren und besitzt keine physische Länge. Die Schildkröte
ignoriert es einfach.
Bemerkenswert sind die verschiedenen Arten der Verzweigung. Ebenfalls
gut sichtbar ist hier das Prinzip der Selbstähnlichkeit: Einzelne
Äste haben stets dieselbe Form wie die gesamte Pflanze.
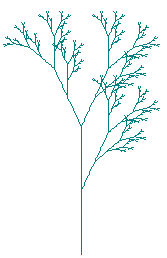
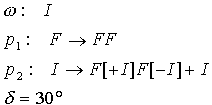
Bild N° 6: Krautige Struktur
Hier ein L-System mit zwei Elementen F und G. F wird als grüne,
G als braune Linie interpretiert. Die Länge der Linien hängt
vom jeweiligen Parameter ab.
Der Parameter bewirkt, dass die Linien kürzer werden, je mehr
sie verzweigt sind.
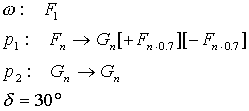
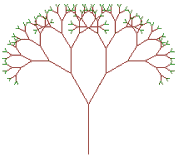
Bild N° 7: Baumartige Struktur (Iterationsstufe 7)
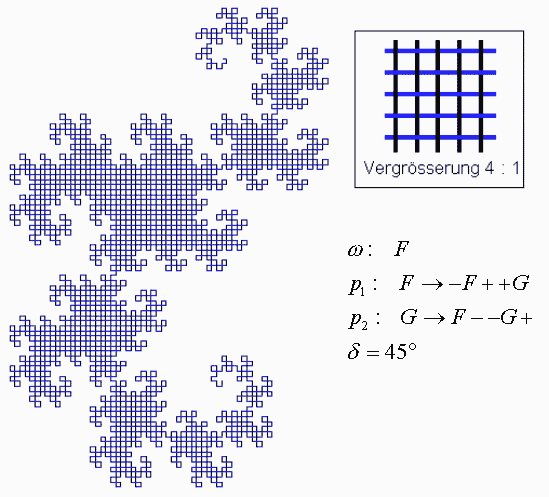
Bild N° 8: Die Drachenkurve
Dass L-Systeme nicht nur pflanzenförmige Strukturen hervorbringen können, zeigt uns dieses klassische Fraktal, das den Namen Drachenkurve erhalten hat. Im kleinen Kasten haben wir einen Ausschnitt aus der Mitte vergrößert, um die Struktur ersichtlich zu machen. (Die Schildkröte zeichnet mit deckender Farbe) Man beachte, dass die gesamte Kurve aus einer einzigen, zusammenhängenden Linie besteht.
Ein nicht deterministisches L-System können wir dadurch erzeugen, dass wir zufällig zwischen 3 Produktionsregeln auswählen. Die Pfeile über den Zahlen geben die Wahrscheinlichkeit an, mit der die betreffende Produktionsregel gewählt wird. In diesem Fall alle mit der gleichen.
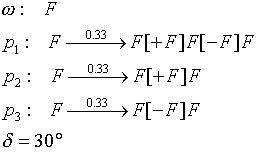
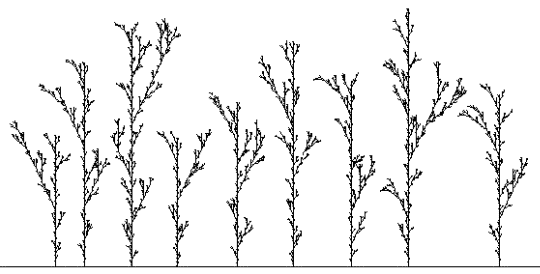
Bild N° 9: Einige mögliche Ausgaben des nichtdeterministischen L-Systems.
Bevor wir zu den kontextabhängigen L-Systemen kommen, wollen wir die bisherigen Ergebnisse auf den Computer übertragen. Das Programm wird uns als Grundlage für alle weiteren dienen. Es besteht aus folgenden grundlegenden Teilen.

Wie wir bereits im Kapitel "Über die Gültigkeit von Simulationen" dargelegt haben, kann das bloße Vergleichen von Endresultaten zu schlimmen Fehlern führen. Obwohl die krautigen, buschigen und baumartigen Figuren stark an Kräuter, Büsche und Bäume erinnern, heißt das nicht unbedingt, dass sie auch dieselbe Konstruktionstopologie haben.
Es empfiehlt sich also, wie bei Anabaena Catenula, das Original in der Natur zu studieren.
Es folgt das Flussdiagramm und anschließend der Text des Programms:
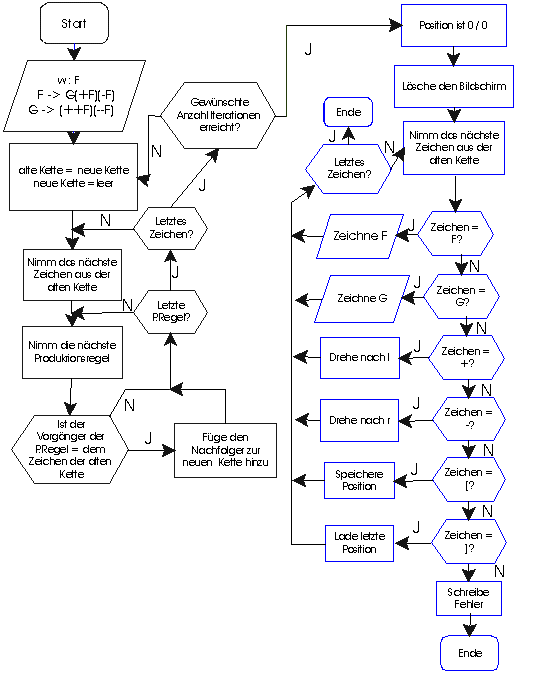
'Definitionen
Const Max_Klammern = 20 'Maximale
Anzahl geöffneter Klammern
Const Anz_ProdRegeln = 5 'Anzahl Produktionsregeln
Const Pi = 3.1415926435 'PI
Dim Axiom As String 'Axiom
Dim a(Anz_ProdRegeln) As String * 1 'Vorgänger a
Dim x(Anz_ProdRegeln) As String 'Nachfolger x
Dim Delta As Single 'Winkel
Dim
KetteNeu As String 'Alte Zeichenkette
Dim KetteAlt As String 'Neue
Zeichenkette
Dim xPos(Max_Klammern) As Single 'x-Koordinate der aktuellen Schilkrötenposition
Dim
yPos(Max_Klammern) As Single 'y-Koordinate der aktuellen Schilkrötenposition
Dim Delt(Max_Klammern) As Single 'Winkel
der aktuellen Schilkrötenposition
Dim Klammer As Integer 'Anzahl geöffneter Klammern
Dim i As Integer, j As Integer 'Zähler für Zeichen (i) und Produktionsregeln (j)
Private Sub Form_Load()
Axiom = "F"
a(0) = "F": x(0) = "G(+F)(-F)"
a(1) = "G": x(1) = "G(++F)(--F)"
Delta = 32
KetteNeu = Axiom
End Sub
Private Sub Command1_Click()
'Routine zur Generierung der Zeichenketten
KetteAlt = KetteNeu 'Neue Kette auf Alte Kette überschreiben
KetteNeu = "" 'Neue Kette löschen
Fori = 1 To Len(KetteAlt) 'Nimm jedes Zeichen der alten Kette
For j = 0 To Anz_ProdRegeln 'Nimm jede Produktionsregel
If a(j) = Mid(KetteAlt, i, 1) Then 'Wenn Zeichen der Kette = a dann
KetteNeu = KetteNeu & x(j) 'füge x zur neuen Kette hinzu
GoTo 1
'und springe zur Marke 1
End If 'Ende Wenn
Next j 'Nächste Produktionsregel
KetteNeu = KetteNeu & Mid(KetteAlt, i, 1) 'Füge das Zeichen der alten Kette der neuen hinzu
1 Next i 'Nächstes Zeichen der alten Kette
Text1.Text = KetteNeu 'Anzeigen der neuen Kette
End Sub
Private Sub Command2_Click()
'Interpretationsroutine
xPos(0) = 0 'Anfangswerte auf 0 setzen
yPos(0) = 0
Delt(0) = 0
For i = 1 To Len(KetteNeu) 'Nimm jedes Zeichen der neuen Kette
Select Case Mid(KetteNeu, i, 1) 'Wähle Fall je nach Zeichen
Case "(" 'Zeichen ist (
Klammer = Klammer + 1 'Eine Klammer mehr offen
xPos(Klammer) = xPos(Klammer - 1) 'Merke aktuelle Position
yPos(Klammer) = yPos(Klammer - 1)
Delt(Klammer) = Delt(Klammer - 1)
Case ")" 'Zeichen ist )
Klammer = Klammer - 1 'Eine Klammer weniger
Case "+" 'Zeichen ist +
Delt(Klammer) = Delt(Klammer) + Delta * Pi / 180 'Drehe
nach links
Case "-" 'Zeichen ist -
Delt(Klammer) = Delt(Klammer) - Delta * Pi / 180 'Drehe
nach rechts
Case "F" 'Zeichen ist F
'Zeichne einen roten, kleinen Schritt vorwärts
Picture1.PSet(325 + xPos(Klammer),650 - yPos(Klammer)),RGB(255,0,0)
xPos(Klammer) = xPos(Klammer) + Sin(Delt(Klammer)) * 10
yPos(Klammer) = yPos(Klammer) + Cos(Delt(Klammer)) * 10
Picture1.Line-(325 + xPos(Klammer),650 - yPos(Klammer)),RGB(255,0,0)
Case "G" 'Zeichen ist G
'Zeichne einen gelben, großen Schritt vorwärts
Picture1.PSet (325 + xPos(Klammer), 650 - yPos(Klammer)),RGB(255,255,0)
xPos(Klammer) = xPos(Klammer) + Sin(Delt(Klammer)) * 30
yPos(Klammer) = yPos(Klammer) + Cos(Delt(Klammer)) * 30
Picture1.Line -(325 + xPos(Klammer), 650 - yPos(Klammer)),RGB(255,255,0)
End Select 'Ende Auswahl
Next i 'Nächstes Zeichen