Fractal Home
Fractal Frieze Ornaments - Symmetry I
The Frieze Groups are represented with fractal patterns in my FriezeOrnaments Machine. It's easy to use, so have a try. Filling Frieze Ornaments along an axis in a regular manner, you only have seven types of moves to copy the basic pattern.
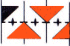
p111
The source code is part of the HTML page with objects in the file canvasimage.js.
Fractal Frieze Ornaments
Ornaments are very important in art and handicraft since a long time. It was already used, when the mathematical background wasn't explored yet. Therefor it is a surprise, that you could find all possible forms in historical art objects, p.e. The Alhambra. The symmetry of Frieze Ornaments is very attractive to nearly everyone.
In a Frieze Ornament there is an axis, to which moves of the basic pattern are made. These moves fill the pattern band. It is proved that there are exactly 7 symmetry groups, called the Frieze Groups, which are described below. The machine ornaments I call Fractal Frieze Ornaments, simply because the basic patterns are of fractal kind.
Complete list of possible transformations
| Type | Description | Visualization |
|---|---|---|
p111 | The basic pattern is moved by a constant amount: It is called a translation or a move translation. |
|
p1g1 | The ornament is filled by continuous use of a combination of a mirror operation and a translation along the ornament's axis. |
|
p112 | The basic pattern is repeated only by 180°-rotations. The center of the rotations are located on the ornament's axis. |
|
pm11 | Only reflections at lines orthogonal to the ornament's axis are needed for this result. |
|
p1m1 | Similiar to type p1g1, but the result of the mirror operation is part of the ornament. |
|
pmg2 | The start is like the beginning of type p112, followed by a reflection at a line orthogonal to the ornament's axis. |
|
pmm2 | The new Frieze Ornament's parts are produced by a combination of two mirror operations, one at the ornament's axis followed by a reflection at a line orthogonal to it. |
|