Fractal Home
More about the L-System Machine
In the year 1968 the german biologist Aristid Lindenmayer developed a model, demonstrating plant's growth with the use of some "construction rules", today named L-System.
L-System basics
The basic principle is simple: Starting with the axiom as the first element, the construction rules form complex expressions which have to be drawn. We only need line elements of a fixed basic length (F, G). In addition there are rotations by a standard angle.
The growing machine is controlled by up to two construction rules. These rules induce the exchange of single symbols by longer expressions and form a more detailed construction. The new expression contains the same symbols, so the following step has to replace them again. The number of steps is called the level (order). The final expression forms the drawing with line elements, rotations and unvisible jumps. Watch the example:

von Koch curve
Axiom: F
Rule: F→F+F−−F+F
Order:
- 0: F
- 1: F+F−−F+F
- 2: F+F−−F+F+F+F−−F+F−−F+F−−F+F+F+F−−F+F
- 3: ...
Every F is replaced by F+F−−F+F, the other symbols remain unchanged.
Download lsystem.js (watch the HTML source code of the previous page). KineticJS is used for the movable point.
List of the most important symbols
| Symbol | Description | Symbol | Description |
|---|---|---|---|
f | move forward one base length without painting |
F, G | move forward one base length with painting |
+ | rotate left by the standard angle |
− | rotate right by the standard angle |
( | save position and direction, multiply the base length by the standard factor |
) | restore position and direction, divide the base length by the standard factor |
[ | save position and direction |
] | restore position and direction |
* | multiply the base length by the standard factor |
/ | divide the base length by the standard factor |
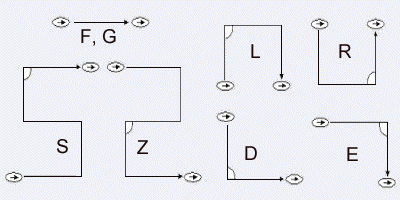
Basic signs F, G and additional symbols
The essay "Wachstumssimulationen" describes the background of the L-System in a more precise manner. Perhaps you'll be able to transform the terms for using them with my machine. Sorry, the essay is only available in german.
