Fractal Home
Creation of Fractal Plantations
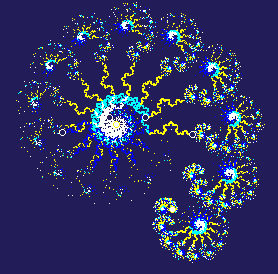
Kochwirbel versus..
Understanding what I call Fractal Plantations depends on the knowledge of Iterated Functions Systems (IFS) and the chaos game. In the WWW you'll find many essays and programs for discovering these objects. Watch my sections Iterations und IFS II p. e. If you are able to understand german, read the hints in the german version.
In my machine two independent IFS are used to create Fractal Plantations. The figure IFS builts the base figure, which is transformed by the hierarchy system. The hierarchy system also is an IFS (but must not be an IFS). If the hierarchy system is a single mathematical function, p.e. a rotation, the chaos game would show only a single point, the fixed point of the rotation. Or if the hierarchy IFS is an usual IFS, p.e. a Koch curve IFS, you'll see the well known Koch curve as the chaos game's result.
The Javascript source codes are if.js and kondchaosgame.js (watch the HTML source code of the previous page, too).

..Wirbelkoch
But now the figure IFS is called first and shows a point of its attractor and only those points are used for transformations by the hierarchy IFS. So the figure IFS forms a condensation set for the hierarchy IFS. The bigger structures of the image therefor show smaller versions of the base figure, as long as the hierarchy IFS hasn't a too high probability in use.
Finally every condensation set would be resulted by the attractor of the "overused" hierarchy set. Because the sense of the plantation images is to get a construction of two coexisting IFS, both IFS need to have their full scope.
Thanks to Eric Rowell for the library KineticJS.
