Fractal Home
Self-organization of vectors
In many dynamic systems structures are formed by self-organization. Here the objects are bivectors (math.: bivectors in geom. algebra), whose data are changed in discrete time steps according to a specific algorithm. A suitable geometrical interpretation results in interesting structures.
The bivectors are interpreted as two points in the n-dimensional Euclidian space (position vectors), where the dimension is determined by the number of components. In an iteration step, the two points are shifted antiparallel (in the opposite direction) by a unit vector. If the two points had a mass, the physical interpretation would be that the center of gravity and the torque of the system remained constant.
Depending on the bivectors set, the displacement vector and the dimension, a variable point cloud is created, which may have an attractor.
- Attractor Gallery
- Structures built by the programs Particle.jar and Attractor.jar
-
-
-
-
-
-
-
-
-
-
-
-
- Structures built by the programs Particle.jar and Attractor.jar
Four bivectors are used in this example (watch the graph above).
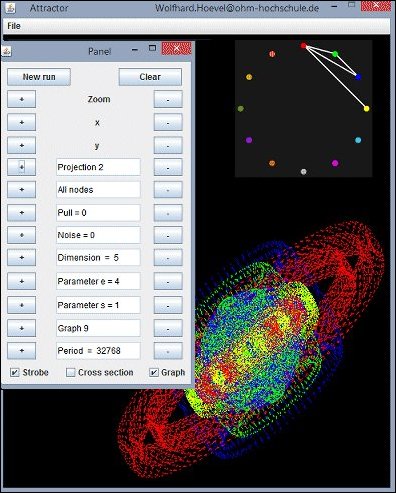
Screenshot of Attractor.jar
The basic algorithm
is described in detail in Hövel's documentation Self-organization of vectors.
Two java programs
with specific configurations are available for download:
Attractor.jar builts structures depending on coupled bivectors.
Particle.jar is an enhancement of Attractor.jar, containing some isolated
coupled bivectors, called particles.
The vectors itself (position vectors) are weakly coupled, what can be interpreted as the effect of electrostatic forces between them.
The interactive page 2 is dedicated to perform own experiments.
The author
Algorithms and programs written by Wolfhard Hövel.
The Graph
provides an overview of the number of points, the bivectors and the particles used in the algorithm. Particles are connected parts of the graph. If there are parts that are not connected with others, there is more than one particle.
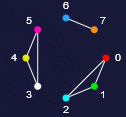
This picture, drawn by the EightPoints machine (page 2) shows that 8 points and
a total of 7 bivectors, spread over 3 particles are used (example no. 18).