Fractal Home
Hyperbolische Ornamente
Der niederländische Grafiker M. C. Escher (1898-1972) hat zahlreiche Werke geschaffen, die immer noch starke Beachtung finden und vor allem Freunde der Mathematik ansprechen. Escher wurde durch den befreundeten Mathematiker Harold S. M. Coxeter inspiriert und ein Ergebnis ist eine Reihe von Werken mit den Titeln Kreislimit I - IV. Mathematisch gesehen handelt es sich bei diesen Werken um Hyperbolische Ornamente.
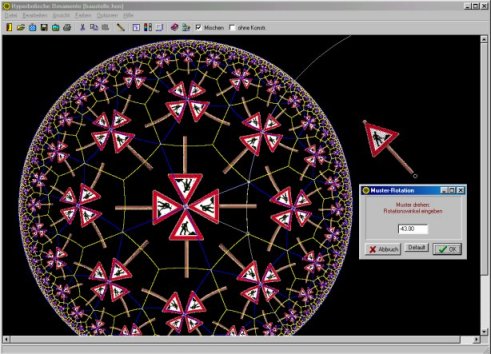
Programm "Hyperbolische Ornamente"
Hyperbolische Fraktal-Ornamente
Die Zeichenfläche ist dem Prinzip nach ein Einheitskreis, der im Idealfall
vollständig mit sich nicht überschneidenden Mustern gefüllt werden kann.
Die Kachelung des Kreises entsteht durch iteratives Spiegeln eines Grundmotivs an den Seiten
eines hyperbolischen Dreiecks, das im Einheitskreis liegt. Iterativ heißt, dass die
Spiegelbilder ebenfalls am Ausgangsdreieck gespiegelt werden. Motive können
die Seiten des Ausgangsdreiecks selbst sein, aber auch ein eingefügtes Bild ist geeignet.
Im hyperbolischen Dreieck ist die dritte Seite Teil eines Kreisbogens. Eine der Spiegelungen
ist also eine Kreisspiegelung, die das Motiv verformt. Wenn alle Regeln eingehalten werden,
bleibt die Folge der Spiegelungen innerhalb des Einheitskreises und es entsteht ein kreisförmiges Ornament.
Die hier gezeigten Darstellungen enthalten fraktale Motive, so dass man die Ergebnisse
fraktale hyperbolische Ornamente nennnen darf.
Das Programm
Mit dem Programm "Hyperbolische Ornamente" wurden alle Grafiken dieser Seite erstellt. Die Bedienung des Programms und der mathematische Hintergrund werden in einer beiliegenden Datei behandelt. Nach der Eingabe von wenigen Parametern kann man die Basiskonstruktion zeichnen lassen. Man kann eine kleine Grafik aus beliebiger Quelle importieren, um sie als Kachel zu verwenden. Mit der Maus wird die Lage des Motivs bestimmt und die Ornamentgröße beeinflusst. Die Importgrafik kann man stufenlos drehen. Das Programm können Sie im Tausch gegen ihr selbst geschriebenes Produkt zum Download bestellen.
Fortsetzung
Auf der nächsten Seite: Interaktive Maschine und etwas Hintergrundtheorie..




