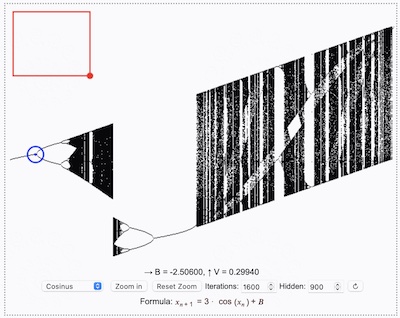
Man bewegt das Zoom-Rechteck und legt seine Größe mit dem roten Punkt fest. Dann klickt man Zoom in und wartet auf die Fertigstellung des Bildes. Mit dem roten Kreis erkennt man die Werte A, B am ausgewählten Punkt.

Der Quellcode ist liapunov.js. Ein Dank geht an Eric Rowell für KineticJS. Beachten Sie ebenfalls den HTML-Code.

Zum Verständnis der Liapunov-Diagramme

Lesen Sie zuerst den Feigenbaum-Text. Die Abbildung rechts zeigt das Feigenbaum-Diagramm des Cosinus-Iterators.

Die Liapunov-Maschine berechnet die Liapunov-Exponenten für die Iteratorfunktion und setzt das Ergebnis in Farben um; es entsteht das Liapunov-Diagramm. Der Liapunov-Exponent macht eine Aussage über die Geschwindigkeit der Änderung der Werte $x_n$ während der Iteration, wenn der Systemparameter $R$ verändert wird. In Ordnungsbereichen ist die Geschwindigkeit niedrig (rot), dagegen hoch in Chaosbereichen (blau).

Die Werte $A$ und $B$ werden in den Systemparameter $R$ während der Iteration und Berechnung des Liapunov-Exponenten eingesetzt, wobei sie einer vorgegebenen Sequenz (z.B. $ABBA$) folgen. Dies erfolgt bei der Farbbestimmung eines jeden Pixels des Bildes. Die benutzten Werte $A, B$ lassen sich in der Maschine mit dem beweglichen roten Kreis erkunden.